Geometri har ursprung i de tidiga civilisationerna som ett praktiskt sätt att hantera längder, area och volym. Geometri började bli en formel matematisk vetenskap i väst så tidigt som 600 år f.Kr. I modern tid har geometri blivit en icke abstrakt form av vetenskap på grund av att den inte längre bara beskriver det som faller inom normala människors erfarenheter.

Olika begrepp inom geometrin

Axiom som är något som Euclid introducerade i geometrin. Axiom faller inom det spektrum att geometri ska vara självbevisande. Euclid gav vissa specifika axioms som han menade var självklara sanningar på grund av att de bevisade sig själva. Dessa var ofta egenskaper som punkter, linjer och plan. Enligt Euclid visar de hur man får fram det matematiskt resonemang som krävs inom geometrin.

Punkter är något av det mest fundamentala och grundläggande inom geometrin, punkter har blivit definierade på många olika sätt. Euclids definition kallas för ”det som inte har någon del” och menar att man genom algebra och andra sätt ger man värde till punkten. Alla objekt är byggda från punkter med undantag från de geometriska lärorna som helt saknar punkter.

Linjer är en av grundstenarna inom geometrin och med en liknande status som punkter. I modern matematik med olika typer av geometri är linjen väldigt sann mot hur hela geometrin fungerar. Exempelvis i analytisk geometri är en linje ett plan som definierar två punkter vars koordinater har givits en linjär ekvation. Men inom en mer abstrakt miljö skulle en linje istället kunna vara ett självständigt objekt ej relevant gentemot de punkter den vilar på.

Plan är ett två dimensionell plan yta som sprider sig oändligt lång i två olika riktningar. Exempelvis studeras plan under topologiska former därför refererar man inte till varken distansen eller riktning. De som studerar plan som yta kan konstatera att vissa saker kan mätas medans andra inte kan det.

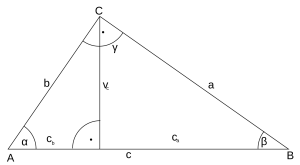
En vanlig Vinkel definieras av Euclid som lutning där två linjer möter varandra i ett plan. En vinkel kräver att linjerna inte ligger rakt i respekt mot varandra. Ett mer modernt sätt att beskriva vinklar som två strålar vars sidor är vinklade i sin relation till varandra och har en gemensam slutpunkt som vertex. Euclid använde vinklar för att studera polygon och trianglar. Studiet av vinklarna i en triangel eller i en cirkel bildar grunden för trigonometri. En stor skillnad mellan geometri och kalkyl är att vinklarna mellan kurvor och ytor kan tas fram med hjälp av derivatan.

Kurvor är 1-dimensionella objekt som kan vara raka som en linje beroende på ekvationen. Kurvor kan också vara en 2-dimensionell kurva som kallas för en jämn kurva eller en 3-dimensionell kurva.

Ytor definieras oftast som ett tvådimensionellt objekt som exempelvis en sfär. Som är en yta som kan exempelvis en sfär definieras parametriskt. I skillnaden mellan geometri och topologi är ytor beskrivna som två dimensionella fläckar som är uppbyggda av ekvationer.

Manifold är generell beskrivning av begrepp relevanta kring kurvor och ytor. En manifold är topologisk rymd där alla punkter har en granne som hela tiden sträcker ut.  Manifolds använder sig av fysik, då ofta generella läror om relativitet men också strängteori.